
문제
라그랑주는 1770년에 모든 자연수는 넷 혹은 그 이하의 제곱수의 합으로 표현할 수 있다고 증명하였다. 어떤 자연수는 복수의 방법으로 표현된다. 예를 들면, 26은 5^2과 1^2의 합이다; 또한 4^2 + 3^2 + 1^2으로 표현할 수도 있다. 역사적으로 암산의 명수들에게 공통적으로 주어지는 문제가 바로 자연수를 넷 혹은 그 이하의 제곱수 합으로 나타내라는 것이었다. 1900년대 초반에 한 암산가가 15663 = 125^2 + 6^2 + 1^2 + 1^2라는 해를 구하는데 8초가 걸렸다는 보고가 있다. 좀 더 어려운 문제에 대해서는 56초가 걸렸다: 11339 = 105^2 + 15^2 + 8^2 + 5^2.
자연수 n이 주어질 때, n을 최소 개수의 제곱수 합으로 표현하는 컴퓨터 프로그램을 작성하시오.
입력
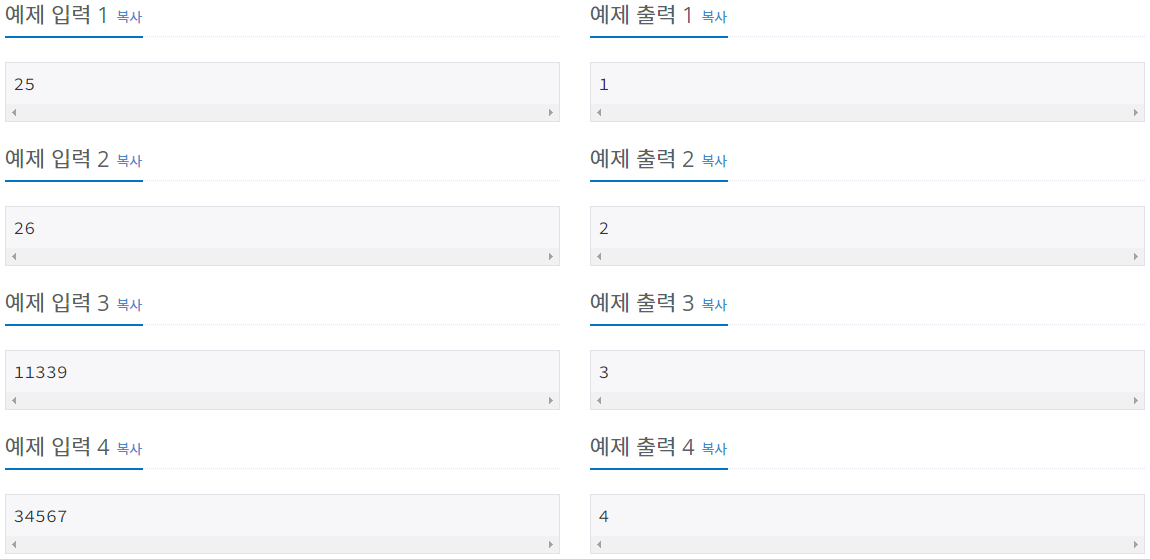
입력은 표준 입력을 사용한다. 입력은 자연수 n을 포함하는 한 줄로 구성된다. 여기서, 1 ≤ n ≤ 50,000이다.
출력
출력은 표준 출력을 사용한다. 합이 n과 같게 되는 제곱수들의 최소 개수를 한 줄에 출력한다.
문제 접근 방법
이번 문제는 다이나믹 프로그래밍(Dynamic Programming)과 브루트 포스 알고리즘(Brute Force AL)을 합친 문제이다.
입력이 들어오면 해당 수까지의 최소 경우의 수를 따져주어야 한다.
DP점화식은 다음과 같다.
dp [idx] = dp [idx-1]+1;으로 초기화를 해준다. (+1을 해 준 이유는 1^2를 해줬다는 가정)
이후에 1~idx사이에 존재하는 제곱수를 이용해서 Math.min(dp [idx], [i-제곱수] +1);로 dp [idx]의 최솟값을 저장해나가면서 idx가 입력수가 될 때까지 진행해준다.
모든 연산이 끝나면 dp [입력수]에는 합을 이루는 제곱수의 최소의 개수가 저장되어 있으므로 이를 출력해주면 된다.
JAVA 코드 풀이
코드 실행 결과

후기
이번 문제도 점화식을 세우기가 조금 힘들었다. 처음에는 해당 수를 만들 수 있는 제곱수의 모든 경우의 수를 따져서 확인해야 한다 생각했었는데 그것이 아니라 이전에 구해놨던 최소 개수에서 추가적으로 제곱수를 더해 만들어야 한다 (= [idx-제곱수]+1)는 것을 깨닫고 문제를 풀 수 있게 되었다.
문제 원본
https://www.acmicpc.net/problem/17626
17626번: Four Squares
라그랑주는 1770년에 모든 자연수는 넷 혹은 그 이하의 제곱수의 합으로 표현할 수 있다고 증명하였다. 어떤 자연수는 복수의 방법으로 표현된다. 예를 들면, 26은 52과 12의 합이다; 또한 42 + 32 + 1
www.acmicpc.net
알고리즘 분류
'문제 풀이 > [JAVA_자바] 백준' 카테고리의 다른 글
| [JAVA / 자바] 백준(BOJ) 1780번 - 종이의 개수 (실버 3) (0) | 2022.03.24 |
|---|---|
| [JAVA / 자바] 백준 16928번 - 뱀과 사다리 게임 (실버 1) (0) | 2022.03.23 |
| [JAVA / 자바] 백준 5525번 - IOIOI (실버 2) (0) | 2022.03.21 |
| [JAVA / 자바] 백준 7662번 - 이중 우선순위 큐 (골드 5) (0) | 2022.03.18 |
| [JAVA / 자바] 백준 9019번 - DSLR (골드 4) (0) | 2022.03.17 |