Kruskal 알고리즘
: 최소 비용 신장 부분 트리를 찾는 알고리즘
최소 비용 신장 트리(MST, Minimum Cost Spanning Tree)의 의미를 모른다면 다음 게시물을 참고하길 바란다.
[자료구조] 최소 비용 신장 트리 (Minimum Cost Spanning Tree)
[자료구조] 신장 트리 (Spanning Tree : ST) 와 최소 비용 신장 트리 (Minimum Cost Spanning Tree : MST)
신장 트리(Spanning Tree : ST) - n개의 정점으로 이루어진 무방향 그래프에서 n개의 모든 정점과 n-1개의 간선으로 만들어진 트리 깊이 우선 신장 트리(Depth First Spanning Tree) / 너비 우선 신장 트리(Bre..
kwin0825.tistory.com
Kruskal 알고리즘 I
- 가중치가 가장 높은 간선부터 제거하면서 최소 비용 신장 트리를 만드는 방법
① 그래프의 모든 간선을 가중치에 따라 내림차순으로 정리한다
② 그래프에서 가중치가 가장 높은 간선을 제거한다 (이때 정점을 그래프에서 분리시키는 간선은 제거할 수 없으므로 이런 경우는 그다음으로 가중치가 높은 간선을 제거)
③ 그래프에 n-1개의 간선만 남을 때까지 ②반복한다
④ 그래프에 n-1의 간선이 남게 되면 최소 비용 신장 트리가 완성된다

Kruskal Algorithm I 연산 과정
Kruskal 알고리즘 II
- 가중치가 가장 낮은 간선부터 삽입하면서 최소 비용 신장 트리를 만드는 방법
① 그래프의 모든 간선을 가중치에 따라 오름차순으로 정리한다
② 그래프에서 가중치가 가장 낮은 간선을 삽입한다 (이때 사이클을 형성하는 간선은 삽입할 수 없으므로 이런 경우는 그다음으로 가중치가 작은 간선 삽입)
③ 그래프에 n-1개의 간선을 삽입할 때까지 ②반복한다
④ 그래프에 간선의 개수가 n-1개가 되면 최소 비용 신장 트리가 완성된다

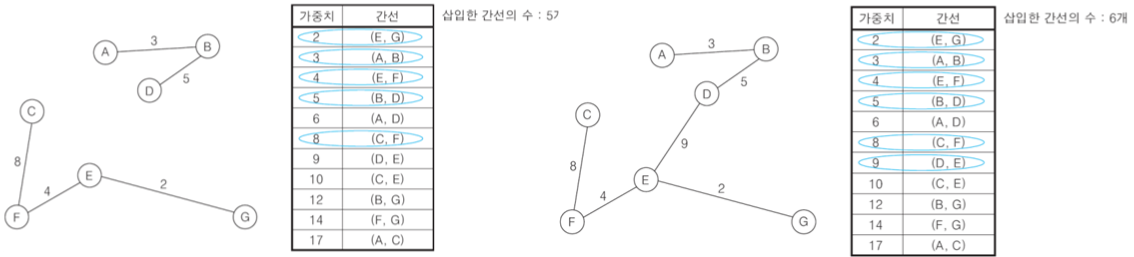
Kruskal Algorithm II 연산 과정
Java 코드
- Kruskal Al II + ArrayList <Edge>
import java.util.*;
import java.io.*;
public class Main {
static int vNum, parent[];
public static void main(String args[]) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer init = new StringTokenizer(br.readLine());
vNum = Integer.parseInt(init.nextToken());
int eNum = Integer.parseInt(init.nextToken());
parent = new int[vNum+1];
ArrayList<Edge> eList = new ArrayList<>();
while(eNum-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine());
eList.add(new Edge(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())));
}
Collections.sort(eList, new Comparator<Edge>() { // 간선의 가중치를 기준으로 오름차순으로 정렬
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
});
System.out.println(kruskal_II(eList));
}
static class Edge implements Comparable<Edge> { // Edge(간선) 클래스
int v1; // 정점 v1
int v2; // 정점 v2
int weight; // 가중치
Edge(int v1, int v2, int w) { // 선언(초기화) 함수
this.v1 = v1;
this.v2 = v2;
this.weight = w;
}
@Override
public int compareTo(Edge e) { // 정렬 시 기준을 무엇으로 삼을지 정해주는 함수
if(this.weight < e.weight)
return -1;
else if(this.weight == e.weight)
return 0;
else
return 1;
}
}
// 간선의 가중치가 제일 작은것부터 그래프에 사이클이 생기지 않게 정점을 연결하는 간선을 삽입
static int kruskal_II(ArrayList<Edge> eList) {
int result = 0, cnt = 0;
for(int i=0; i<eList.size(); i++) {
if(union(eList.get(i).v1, eList.get(i).v2)) { // 그래프에 사이클이 생기는 간선인지 확인
result += eList.get(i).weight; // 최소 신장 트리를 구성하는 간선이므로 출력할 결과값에 더해준다
cnt++; // 최소 신장 트리를 구성하는 간선을 찾은 횟수를 카운트 하는 변수
}
if(cnt == vNum-1) // 최소 신장 트리를 찾았으면 반복문을 멈춘다
break;
}
return result;
}
public static int find(int v) { // 정점 v의 부모를 찾는 함수
if(parent[v] == 0)
return v;
return parent[v] = find(parent[v]);
}
public static boolean union(int v1, int v2) {
int v1P = find(v1); // 정점 v1의 부모가 되는 정점을 찾는다.
int v2P = find(v2); // 정점 v2의 부모가 되는 정점을 찾는다.
// 두 정점의 부모가 다르다는 것은 그래프에 사이클이 없다는것을 의미
if(v1P != v2P) {
parent[v2P] = v1P;
return true;
}
return false;
}
}
- Kruskal Al II + 인접 행렬
import java.util.*;
import java.io.*;
public class Main {
static int vNum, parent[];
public static void main(String args[]) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer init = new StringTokenizer(br.readLine());
vNum = Integer.parseInt(init.nextToken());
int eNum = Integer.parseInt(init.nextToken());
parent = new int[vNum+1];
int eList[][] = new int[eNum][3];
for(int i=0; i<eNum; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j=0; j<3; j++)
eList[i][j] = Integer.parseInt(st.nextToken());
}
Arrays.sort(eList, new Comparator<int[]>() { // 간선의 가중치를 기준으로 오름차순으로 정렬
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
System.out.println(kruskal_II(eList));
}
// 간선의 가중치가 제일 작은것부터 그래프에 사이클이 생기지 않게 정점을 연결하는 간선을 삽입
static int kruskal_II(int[][] eList) {
int result = 0, cnt = 0;
for(int i=0; i<eList.length; i++) {
if(union(eList[i][0], eList[i][1])) { // 그래프에 사이클이 생기는 간선인지 확인
result += eList[i][2]; // 최소 신장 트리를 구성하는 간선이므로 출력할 결과값에 더해준다
cnt++; // 최소 신장 트리를 구성하는 간선을 찾은 횟수를 카운트 하는 변수
}
if(cnt == vNum-1) // 최소 신장 트리를 찾았으면 반복문을 멈춘다
break;
}
return result;
}
public static int find(int v) { // 정점 v의 부모를 찾는 함수
if(parent[v] == 0)
return v;
return parent[v] = find(parent[v]);
}
public static boolean union(int v1, int v2) {
int v1P = find(v1); // 정점 v1의 부모가 되는 정점을 찾는다.
int v2P = find(v2); // 정점 v2의 부모가 되는 정점을 찾는다.
// 두 정점의 부모가 다르다는 것은 그래프에 사이클이 없다는것을 의미
if(v1P != v2P) {
parent[v2P] = v1P;
return true;
}
return false;
}
}시간 복잡도
- O(E*log V)
* V = 정점의 수, E = 간선(노드)의 수
크루스칼 알고리즘과 유사한 알고리즘
- [알고리즘] 프림 알고리즘(Prim Algorithm) - JAVA / 자바
[알고리즘] 프림 알고리즘(Prim Algorithm) - JAVA / 자바
프림 알고리즘(Prim Algorithm) : 가중치가 있는 무향(방향X) 그래프의 최소 비용 신장 트리(MST)를 찾는 알고리즘 최소 비용 신장 트리(MST, Minimum Cost Spanning Tree)의 의미를 모른다면 다음 게시물을 참고
kwin0825.tistory.com
'알고리즘 > [JAVA_자바] 알고리즘' 카테고리의 다른 글
| [알고리즘] 삽입 정렬 (Insert Sort) - JAVA / 자바 (0) | 2022.01.30 |
|---|---|
| [알고리즘] 퀵정렬 (Quick Sort) - JAVA / 자바 (0) | 2022.01.30 |
| [알고리즘] 버블 정렬 (Bubble Sort) - JAVA / 자바 (0) | 2022.01.30 |
| [알고리즘] 선택 정렬 (Selection Sort) - JAVA / 자바 (0) | 2022.01.30 |
| [알고리즘] 프림 알고리즘(Prim Algorithm) - JAVA / 자바 (0) | 2022.01.29 |