728x90
반응형
다익스트라 알고리즘(Dijkstra Algorithm)
: 음의 가중치가 없는 가중 그래프에서의 최단 경로를 구하는 알고리즘
특징
① 그래프에서 음의 가중치가 없어야 한다. ( ↔ 플로이드-와샬 알고리즘 (Floyd-Warshall Algorithm))
알고리즘
① V1부터 Vn까지 연결된 간선 인접 행렬 또는 인접 리스트에 저장
② V1부터 방문하여 V1에서 갈 수 있는 정점에 대해 최소 거리 갱신 및 다음 방문 예정지로 저장

| V1 | V2 | V3 | V4 | V5 | |
| V1 | 0 | 1 | 2 | 5 | INF |
| V2 | 1 | 0 | 2 | 3 | INF |
| V3 | 2 | 2 | 0 | INF | 4 |
| V4 | 5 | 3 | INF | 0 | 1 |
| V5 | INF | INF | 4 | 1 | 0 |
더보기

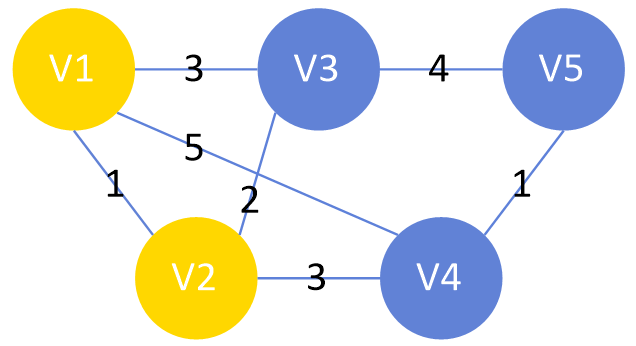
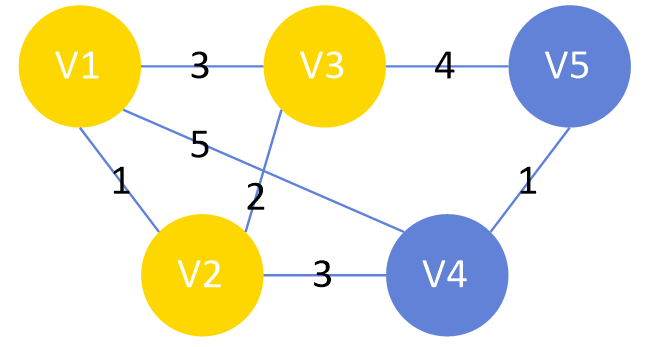

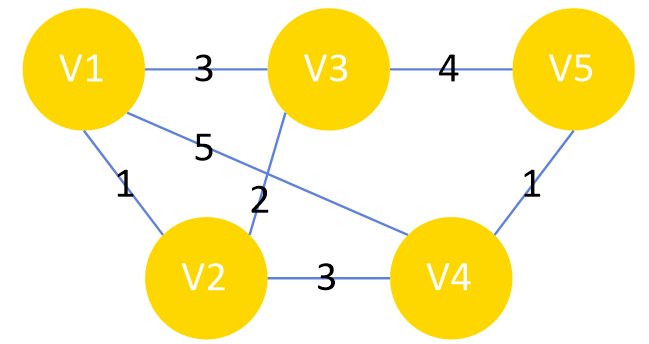

| V1 | V2 | V3 | V4 | V5 | |
| V1 | 0 | 1 | 3 | 5 | INF |

| V1 | V2 | V3 | V4 | V5 | |
| V1 | 0 | 1 | 3 | INF |

| V1 | V2 | V3 | V4 | V5 | |
| V1 | 0 | 1 | 3 | 4 |

| V1 | V2 | V3 | V4 | V5 | |
| V1 | 0 | 1 | 3 | 4 |

| V1 | V2 | V3 | V4 | V5 | |
| V1 | 0 | 1 | 3 | 4 | 5 |
Java 코드 구현
public static int[] dijkstra(int sV) {
PriorityQueue<Node> pQueue = new PriorityQueue<>();
pQueue.add(new Node(sV, 0));
boolean visited[] = new boolean[n+1];
int distance[] = new int[n+1];
Arrays.fill(distance, Integer.MAX_VALUE);
distance[sV] = 0;
Node n;
while(!pQueue.isEmpty()) {
n = pQueue.remove();
if(visited[n.v])
continue;
visited[n.v] = true;
for(Node i : map[n.v])
if(distance[n.v] + i.w < distance[i.v]) {
distance[i.v] = distance[n.v] + i.w;
pQueue.add(new Node(i.v, distance[i.v]));
}
}
return distance;
}시간 복잡도
- 우선순위 큐 = O((V+E) log V)
- 인접 행렬 = O(V^2)
- 연결 그래프 = O(Elog V)
*V = 정점의 수, E = 간선의 수
대표적인 플루이드-와샬 알고리즘 사용 예
- (음수 가중치가 없는) 가중 그래프에서의 최단 경로 탐색
728x90
반응형
'알고리즘 > [JAVA_자바] 알고리즘' 카테고리의 다른 글
| [알고리즘] 0-1 너비 우선 탐색 알고리즘 (0-1 Breath First Search Algorithm, 0-1 BFS) - JAVA / 자바 (0) | 2022.03.05 |
|---|---|
| [알고리즘] 0-1 배낭 문제 (0-1 Knapsack Problem) - JAVA / 자바 (0) | 2022.02.27 |
| [알고리즘] 플로이드-와샬 알고리즘 (Floyd-Warshall Algorithm) - JAVA / 자바 (0) | 2022.02.20 |
| [알고리즘] 너비 우선 탐색 (Breath First Search, BFS) - JAVA / 자바 (0) | 2022.02.19 |
| [알고리즘] 깊이 우선 탐색 (Depth First Search, DFS) - JAVA/자바 (0) | 2022.02.13 |